MAXimal
добавлено: 13 Aug 2010 19:48
редактировано: 14 Jun 2012 5:01
Содержание [скрыть]
Алгоритм Диница
Постановка задачи
Пусть дана сеть, т.е. ориентированный граф 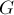 , в котором каждому ребру
, в котором каждому ребру 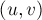 приписана пропускная способность
приписана пропускная способность 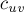 , а также выделены две вершины — исток
, а также выделены две вершины — исток  и сток
и сток  .
.
Требуется найти в этой сети поток 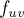 из истока
из истока  в сток
в сток  максимальной величины.
максимальной величины.
Немного истории
Этот алгоритм был опубликован советским (израильским) учёным Ефимом Диницем (Yefim Dinic, иногда пишется как "Dinitz") в 1970 г., т.е. даже на два года раньше опубликования алгоритма Эдмондса-Карпа (впрочем, оба алгоритма были независимо открыты в 1968 г.).
Кроме того, следует отметить, что некоторые упрощения алгоритма были произведены Шимоном Ивеном (Shimon Even) и его учеником Алоном Итаи (Alon Itai) в 1979 г. Именно благодаря им алгоритм получил свой современный облик: они применили к идее Диница концепцию блокирующих потоков Александра Карзанова (Alexander Karzanov, 1974 г.), а также переформулировали алгоритм к той комбинации обхода в ширину и в глубину, в которой сейчас этот алгоритм и излагается везде.
Развитие идей по отношению к потоковым алгоритмам крайне интересно рассматривать, учитывая "железный занавес" тех лет, разделявший СССР и Запад. Видно, как иногда похожие идеи появлялись почти одновременно (как в случае алгоритма Диница и алгоритма Эдмондса-Карпа), правда, имея при этом разную эффективность (алгоритм Диница на один порядок быстрее); иногда же, наоборот, появление идеи по одну сторону "занавеса" опережало аналогичный ход по другую сторону более чем на десятилетие (как алгоритм Карзанова проталкивания в 1974 г. и алгоритм Гольдберга (Goldberg) проталкивания в 1985 г.).
Необходимые определения
Введём три необходимых определения (каждое из них является независимым от остальных), которые затем будут использоваться в алгоритме Диница.
Остаточной сетью 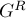 по отношению к сети
по отношению к сети 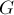 и некоторому потоку
и некоторому потоку 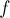 в ней называется сеть, в которой каждому ребру
в ней называется сеть, в которой каждому ребру 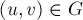 с пропускной способностью
с пропускной способностью 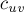 и потоком
и потоком 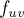 соответствуют два ребра:
соответствуют два ребра:
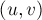 с пропускной способностью
с пропускной способностью 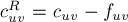
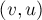 с пропускной способностью
с пропускной способностью 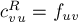
Стоит отметить, что при таком определении в остаточной сети могут появляться кратные рёбра: если в исходной сети было как ребро 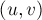 , так и
, так и 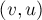 .
.
Остаточное ребро можно интуитивно понимать как меру того, насколько ещё можно увеличить поток вдоль какого-то ребра. В самом деле, если по ребру 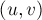 с пропускной способностью
с пропускной способностью 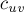 протекает поток
протекает поток 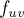 , то потенциально по нему можно пропустить ещё
, то потенциально по нему можно пропустить ещё 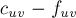 единиц потока, а в обратную сторону можно пропустить до
единиц потока, а в обратную сторону можно пропустить до 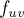 единиц потока, что будет означать отмену потока в первоначальном направлении.
единиц потока, что будет означать отмену потока в первоначальном направлении.
Блокирующим потоком в данной сети называется такой поток, что любой путь из истока  в сток
в сток  содержит насыщенное этим потоком ребро. Иными словами, в данной сети не найдётся такого пути из истока в сток, вдоль которого можно беспрепятственно увеличить поток.
содержит насыщенное этим потоком ребро. Иными словами, в данной сети не найдётся такого пути из истока в сток, вдоль которого можно беспрепятственно увеличить поток.
Блокирующий поток не обязательно максимален. Теорема Форда-Фалкерсона говорит о том, что поток будет максимальным тогда и только тогда, когда в остаточной сети не найдётся 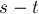 пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети.
пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети.
Слоистая сеть для данной сети строится следующим образом. Сначала определяются длины кратчайших путей из истока  до всех остальных вершин; назовём уровнем
до всех остальных вершин; назовём уровнем ![{\rm level}[v]](../tex2png/cache/3af66db6d15f64d610a605b82168c50f.png) вершины её расстояние от истока. Тогда в слоистую сеть включают все те рёбра
вершины её расстояние от истока. Тогда в слоистую сеть включают все те рёбра 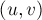 исходной сети, которые ведут с одного уровня на какой-либо другой, более поздний, уровень, т.е.
исходной сети, которые ведут с одного уровня на какой-либо другой, более поздний, уровень, т.е. ![{\rm level}[u] + 1 = {\rm level}[v]](../tex2png/cache/497d21a2cb55c75efb1bb4adddb432d2.png) (почему в этом случае разница расстояний не может превосходить единицы, следует из свойства кратчайших расстояний). Таким образом, удаляются все рёбра, расположенные целиком внутри уровней, а также рёбра, ведущие назад, к предыдущим уровням.
(почему в этом случае разница расстояний не может превосходить единицы, следует из свойства кратчайших расстояний). Таким образом, удаляются все рёбра, расположенные целиком внутри уровней, а также рёбра, ведущие назад, к предыдущим уровням.
Очевидно, слоистая сеть ациклична. Кроме того, любой 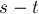 путь в слоистой сети является кратчайшим путём в исходной сети.
путь в слоистой сети является кратчайшим путём в исходной сети.
Построить слоистую сеть по данной сети очень легко: для этого надо запустить обход в ширину по рёбрам этой сети, посчитав тем самым для каждой вершины величину ![{\rm level}[]](../tex2png/cache/d78e498fc2b8304febac57b0be0dcb2e.png) , и затем внести в слоистую сеть все подходящие рёбра.
, и затем внести в слоистую сеть все подходящие рёбра.
Примечание. Термин "слоистая сеть" в русскоязычной литературе не употребляется; обычно эта конструкция называется просто "вспомогательным графом". Впрочем, на английском языке обычно используется термин "layered network".
Алгоритм
Схема алгоритма
Алгоритм представляет собой несколько фаз. На каждой фазе сначала строится остаточная сеть, затем по отношению к ней строится слоистая сеть (обходом в ширину), а в ней ищется произвольный блокирующий поток. Найденный блокирующий поток прибавляется к текущему потоку, и на этом очередная итерация заканчивается.
Этот алгоритм схож с алгоритмом Эдмондса-Карпа, но основное отличие можно понимать так: на каждой итерации поток увеличивается не вдоль одного кратчайшего 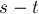 пути, а вдоль целого набора таких путей (ведь именно такими путями и являются пути в блокирующем потоке слоистой сети).
пути, а вдоль целого набора таких путей (ведь именно такими путями и являются пути в блокирующем потоке слоистой сети).
Корректность алгоритма
Покажем, что если алгоритм завершается, то на выходе у него получается поток именно максимальной величины.
В самом деле, предположим, что в какой-то момент в слоистой сети, построенной для остаточной сети, не удалось найти блокирующий поток. Это означает, что сток  вообще не достижим в слоистой сети из истока
вообще не достижим в слоистой сети из истока  . Но поскольку слоистая сеть содержит в себе все кратчайшие пути из истока в остаточной сети, это в свою очередь означает, что в остаточной сети нет пути из истока в сток. Следовательно, применяя теорему Форда-Фалкерсона, получаем, что текущий поток в самом деле максимален.
. Но поскольку слоистая сеть содержит в себе все кратчайшие пути из истока в остаточной сети, это в свою очередь означает, что в остаточной сети нет пути из истока в сток. Следовательно, применяя теорему Форда-Фалкерсона, получаем, что текущий поток в самом деле максимален.
Оценка числа фаз
Покажем, что алгоритм Диница всегда выполняет менее  фаз. Для этого докажем две леммы:
фаз. Для этого докажем две леммы:
Лемма 1. Кратчайшее расстояние от истока до каждой вершины не уменьшается с выполнением каждой итерации, т.е.
![{\rm level}_{i+1}[v] \ge {\rm level}_i[v]](../tex2png/cache/b79ca81f5f477fe54b414571bbf75617.png)
где нижний индекс обозначает номер фазы, перед которой взяты значения этих переменных.
Доказательство. Зафиксируем произвольную фазу  и произвольную вершину
и произвольную вершину  и рассмотрим любой кратчайший
и рассмотрим любой кратчайший 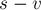 путь
путь  в сети
в сети 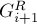 (напомним, так мы обозначаем остаточную сеть, взятую перед выполнением
(напомним, так мы обозначаем остаточную сеть, взятую перед выполнением 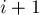 -ой фазы). Очевидно, длина пути
-ой фазы). Очевидно, длина пути  равна
равна ![{\rm level}_{i+1}[v]](../tex2png/cache/1dc8d29487cc3b4eb638f6f3c26b392e.png) .
.
Заметим, что в остаточную сеть 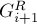 могут входить только рёбра из
могут входить только рёбра из 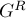 , а также рёбра, обратные рёбрам из
, а также рёбра, обратные рёбрам из 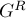 (это следует из определения остаточной сети). Рассмотрим два случая:
(это следует из определения остаточной сети). Рассмотрим два случая:
- Путь
 содержит только рёбра из
содержит только рёбра из 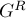 . Тогда, понятно, длина пути
. Тогда, понятно, длина пути  больше либо равна
больше либо равна ![{\rm level}_i[v]](../tex2png/cache/8be2aa8dd31fa8ac98a16b5db0420b03.png) (потому что
(потому что ![{\rm level}_i[v]](../tex2png/cache/8be2aa8dd31fa8ac98a16b5db0420b03.png) по определению — длина кратчайшего пути), что и означает выполнение неравенства.
по определению — длина кратчайшего пути), что и означает выполнение неравенства. - Путь
 содержит как минимум одно ребро, не содержащееся в
содержит как минимум одно ребро, не содержащееся в 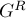 (но обратное какому-то ребру из
(но обратное какому-то ребру из 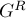 ). Рассмотрим первое такое ребро; пусть это будет ребро
). Рассмотрим первое такое ребро; пусть это будет ребро 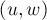 .
.![s \Longrightarrow u \rightarrow w \Longrightarrow[...]](../tex2png/cache/0ccc5c281eb06881f5fabfb4dc61265d.png)
Мы можем применить нашу лемму к вершине
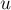 , потому что она подпадает под первый случай; итак, мы получаем неравенство
, потому что она подпадает под первый случай; итак, мы получаем неравенство ![{\rm level}_{i+1}[u] \ge {\rm level}_i[u]](../tex2png/cache/c47967b2d7859e8a4e786f57be15cfda.png) .
.Теперь заметим, что поскольку ребро
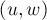 появилось в остаточной сети только после выполнения
появилось в остаточной сети только после выполнения  -ой фазы, то отсюда следует, что вдоль ребра
-ой фазы, то отсюда следует, что вдоль ребра 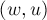 был дополнительно пропущен какой-то поток; следовательно, ребро
был дополнительно пропущен какой-то поток; следовательно, ребро 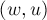 принадлежало слоистой сети перед
принадлежало слоистой сети перед  -ой фазой, а потому
-ой фазой, а потому ![{\rm level}_i[u] = {\rm level}_i[w] + 1](../tex2png/cache/16df0076ca9a5ffff228955c27687d45.png) . Учтём, что по свойству кратчайших путей
. Учтём, что по свойству кратчайших путей ![{\rm level}_{i+1}[w] = {\rm level}_{i+1}[u] + 1](../tex2png/cache/20410a08bea121ad9acee423c9d1875e.png) , и объединяя это равенство с двумя предыдущими неравенствами, получаем:
, и объединяя это равенство с двумя предыдущими неравенствами, получаем:![{\rm level}_{i+1}[w] \ge {\rm level}_i[w] + 2.](../tex2png/cache/764f2ca8d8a03c08093a1508c469dbd7.png)
Теперь мы можем применять те же самые рассуждения ко всему оставшемуся пути до
 (т.е. что каждое инвертированное ребро добавляет к
(т.е. что каждое инвертированное ребро добавляет к 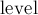 как минимум два), и в итоге получим требуемое неравенство.
как минимум два), и в итоге получим требуемое неравенство.
Лемма 2. Расстояние между истоком и стоком строго увеличивается после каждой фазы алгоритма, т.е.:
![{\rm level}^\prime[t] > {\rm level}[t],](../tex2png/cache/e5cc9b946180e0072f8cf999d90d0c12.png)
где штрихом помечено значение, полученное на следующей фазе алгоритма.
Доказательство: от противного. Предположим, что после выполнения текущей фазы оказалось, что ![{\rm level}^\prime[t] = {\rm level}[t]](../tex2png/cache/92aecf5c0ccb94aedd0c8a92555d1168.png) . Рассмотрим кратчайший путь из истока в сток; по предположению, его длина должна сохраниться неизменной. Однако остаточная сеть на следующей фазе содержит только рёбра остаточной сети перед выполнением текущей фазы, либо обратные к ним. Таким образом, пришли к противоречию: нашёлся
. Рассмотрим кратчайший путь из истока в сток; по предположению, его длина должна сохраниться неизменной. Однако остаточная сеть на следующей фазе содержит только рёбра остаточной сети перед выполнением текущей фазы, либо обратные к ним. Таким образом, пришли к противоречию: нашёлся 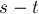 путь, который не содержит насыщенных рёбер, и имеет ту же длину, что и кратчайший путь. Этот путь должен был быть "заблокирован" блокирующим потоком, чего не произошло, в чём и заключается противоречие, что и требовалось доказать.
путь, который не содержит насыщенных рёбер, и имеет ту же длину, что и кратчайший путь. Этот путь должен был быть "заблокирован" блокирующим потоком, чего не произошло, в чём и заключается противоречие, что и требовалось доказать.
Эту лемму интуитивно можно понимать следующим образом: на  -ой фазе алгоритм Диница выявляет и насыщает все
-ой фазе алгоритм Диница выявляет и насыщает все 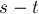 пути длины
пути длины  .
.
Поскольку длина кратчайшего пути из  в
в  не может превосходить
не может превосходить 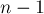 , то, следовательно, алгоритм Диница совершает не более
, то, следовательно, алгоритм Диница совершает не более 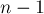 фазы.
фазы.
Поиск блокирующего потока
Чтобы завершить построение алгоритма Диница, надо описать алгоритм нахождения блокирующего потока в слоистой сети — ключевое место алгоритма.
Мы рассмотрим три возможных варианта реализации поиска блокирующего потока:
- Искать
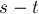 пути по одному, пока такие пути находятся. Путь можно найти за
пути по одному, пока такие пути находятся. Путь можно найти за 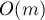 обходом в глубину, а всего таких путей будет
обходом в глубину, а всего таких путей будет 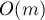 (поскольку каждый путь насыщает как минимум одно ребро). Итоговая асимптотика поиска одного блокирующего потока составит
(поскольку каждый путь насыщает как минимум одно ребро). Итоговая асимптотика поиска одного блокирующего потока составит 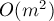 .
. - Аналогично предыдущей идее, однако удалять в процессе обхода в глубину из графа все "лишние" рёбра, т.е. рёбра, вдоль которых не получится дойти до стока.
Это очень легко реализовать: достаточно удалять ребро после того, как мы просмотрели его в обходе в глубину (кроме того случая, когда мы прошли вдоль ребра и нашли путь до стока). С точки зрения реализации, надо просто поддерживать в списке смежности каждой вершины указатель на первое неудалённое ребро, и увеличивать этот указать в цикле внутри обхода в глубину.
Оценим асимптотику этого решения. Каждый обход в глубину завершается либо насыщением как минимум одного ребра (если этот обход достиг стока), либо продвижением вперёд как минимум одного указателя (в противном случае). Можно понять, что один запуск обхода в глубину из основной программы работает за
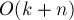 , где
, где  — число продвижений указателей. Учитывая, что всего запусков обхода в глубину в рамках поиска одного блокирующего потока будет
— число продвижений указателей. Учитывая, что всего запусков обхода в глубину в рамках поиска одного блокирующего потока будет 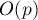 , где
, где 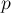 — число рёбер, насыщенных этим блокирующим потоком, то весь алгоритм поиска блокирующего потока отработает за
— число рёбер, насыщенных этим блокирующим потоком, то весь алгоритм поиска блокирующего потока отработает за 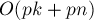 , что, учитывая, что все указатели в сумме прошли расстояние
, что, учитывая, что все указатели в сумме прошли расстояние 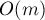 , даёт асимптотику
, даёт асимптотику 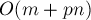 . В худшем случае, когда блокирующий поток насыщает все рёбра, асимптотика получается
. В худшем случае, когда блокирующий поток насыщает все рёбра, асимптотика получается 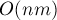 ; эта асимптотика и будет использоваться далее.
; эта асимптотика и будет использоваться далее.Можно сказать, что этот способ нахождения блокирующего потока чрезвычайно эффективен в том смысле, что на поиск одного увеличивающего пути он тратит
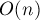 операций в среднем. Именно в этом и кроется разность на целый порядок эффективностей алгоритма Диница и Эдмондса-Карпа (который ищет один увеличивающий путь за
операций в среднем. Именно в этом и кроется разность на целый порядок эффективностей алгоритма Диница и Эдмондса-Карпа (который ищет один увеличивающий путь за 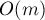 ).
).Этот способ решения является по-прежнему простым для реализации, но достаточно эффективным, и потому наиболее часто применяется на практике.
- Можно применить специальные структуры данных — динамические деревья Слетора (Sleator) и Тарьяна (Tarjan)). Тогда каждый блокирующий поток можно найти за время
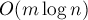 .
.
Асимптотика
Таким образом, весь алгоритм Диница выполняется за 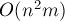 , если блокирующий поток искать описанным выше способом за
, если блокирующий поток искать описанным выше способом за 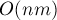 . Реализация с использованием динамических деревьев Слетора и Тарьяна будет работать за время
. Реализация с использованием динамических деревьев Слетора и Тарьяна будет работать за время 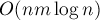 .
.
Единичные сети
Единичной сетью ("unit network") называется такая сеть, в которой пропускные способности всех существующих рёбер равны единице, и у любой вершины, кроме истока и стока, либо входящее, либо исходящее ребро единственно.
Этот случай является достаточно важным, поскольку в задаче поиска максимального паросочетания построенная сеть является именно единичной.
Докажем, что на единичных сетях алгоритм Диница даже в простой реализации (которая на произвольных графах отрабатывает за 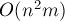 ) работает за время
) работает за время 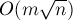 , достигая на задаче поиска наибольшего паросочетания один из лучших известных алгоритмов — алгоритм Хопкрофта-Карпа.
, достигая на задаче поиска наибольшего паросочетания один из лучших известных алгоритмов — алгоритм Хопкрофта-Карпа.
Во-первых, отметим, что приведённый выше алгоритм поиска блокирующего потока, который на произвольных сетях работает за время 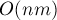 , в сетях с единичными пропускными способностями будет работать за
, в сетях с единичными пропускными способностями будет работать за 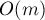 : в силу того, что каждое ребро не будет просмотрено более одного раза.
: в силу того, что каждое ребро не будет просмотрено более одного раза.
Во-вторых, оценим общее количество фаз, которое могло произойти в случае единичных сетей.
Пусть уже было произведено 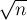 фаз алгоритма Диница; тогда все увеличивающие пути длины не более
фаз алгоритма Диница; тогда все увеличивающие пути длины не более 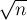 уже обнаружены. Пусть
уже обнаружены. Пусть 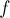 — текущий найденный поток, а
— текущий найденный поток, а 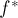 — искомый максимальный поток; рассмотрим их разность:
— искомый максимальный поток; рассмотрим их разность: 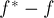 . Она представляет из себя поток в остаточной сети
. Она представляет из себя поток в остаточной сети 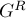 . Этот поток имеет величину
. Этот поток имеет величину 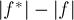 , и вдоль каждого ребра равен нулю или единице. Его можно декомпозировать на набор из
, и вдоль каждого ребра равен нулю или единице. Его можно декомпозировать на набор из 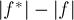 путей из
путей из  в
в  и, возможно, циклов. Поскольку сеть единична, то все эти пути не могут иметь общих вершин, поэтому, учитывая вышесказанное, суммарное количество вершин в них
и, возможно, циклов. Поскольку сеть единична, то все эти пути не могут иметь общих вершин, поэтому, учитывая вышесказанное, суммарное количество вершин в них 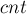 можно оценить как:
можно оценить как:
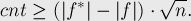
С другой стороны, учитывая, что 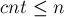 , мы получаем отсюда:
, мы получаем отсюда:
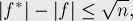
что означает, что ещё через 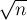 фаз алгоритма Диница гарантированно найдётся максимальный поток.
фаз алгоритма Диница гарантированно найдётся максимальный поток.
Следовательно, общее число фаз алгоритма Диница, выполняемое на единичных сетях, можно оценить как 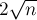 , что и требовалось доказать.
, что и требовалось доказать.
Реализация
Приведём две реализации алгоритма за 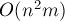 , работающие на сетях, заданных матрицами смежности и списками смежности соответственно.
, работающие на сетях, заданных матрицами смежности и списками смежности соответственно.
Реализация над графами в виде матриц смежности
const int MAXN = ...; // число вершин const int INF = 1000000000; // константа-бесконечность int n, c[MAXN][MAXN], f[MAXN][MAXN], s, t, d[MAXN], ptr[MAXN], q[MAXN]; bool bfs() { int qh=0, qt=0; q[qt++] = s; memset (d, -1, n * sizeof d[0]); d[s] = 0; while (qh < qt) { int v = q[qh++]; for (int to=0; to<n; ++to) if (d[to] == -1 && f[v][to] < c[v][to]) { q[qt++] = to; d[to] = d[v] + 1; } } return d[t] != -1; } int dfs (int v, int flow) { if (!flow) return 0; if (v == t) return flow; for (int & to=ptr[v]; to<n; ++to) { if (d[to] != d[v] + 1) continue; int pushed = dfs (to, min (flow, c[v][to] - f[v][to])); if (pushed) { f[v][to] += pushed; f[to][v] -= pushed; return pushed; } } return 0; } int dinic() { int flow = 0; for (;;) { if (!bfs()) break; memset (ptr, 0, n * sizeof ptr[0]); while (int pushed = dfs (s, INF)) flow += pushed; } return flow; }
Сеть должна быть предварительно считана: должны быть заданы переменные  ,
,  ,
,  , а также считана матрица пропускных способностей
, а также считана матрица пропускных способностей ![c[][]](../tex2png/cache/c82ff706ca1c13812c33e9dd4b08261c.png) . Основная функция решения —
. Основная функция решения — 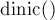 , которая возвращает величину найденного максимального потока.
, которая возвращает величину найденного максимального потока.
Реализация над графами в виде списков смежности
const int MAXN = ...; // число вершин const int INF = 1000000000; // константа-бесконечность struct edge { int a, b, cap, flow; }; int n, s, t, d[MAXN], ptr[MAXN], q[MAXN]; vector<edge> e; vector<int> g[MAXN]; void add_edge (int a, int b, int cap) { edge e1 = { a, b, cap, 0 }; edge e2 = { b, a, 0, 0 }; g[a].push_back ((int) e.size()); e.push_back (e1); g[b].push_back ((int) e.size()); e.push_back (e2); } bool bfs() { int qh=0, qt=0; q[qt++] = s; memset (d, -1, n * sizeof d[0]); d[s] = 0; while (qh < qt && d[t] == -1) { int v = q[qh++]; for (size_t i=0; i<g[v].size(); ++i) { int id = g[v][i], to = e[id].b; if (d[to] == -1 && e[id].flow < e[id].cap) { q[qt++] = to; d[to] = d[v] + 1; } } } return d[t] != -1; } int dfs (int v, int flow) { if (!flow) return 0; if (v == t) return flow; for (; ptr[v]<(int)g[v].size(); ++ptr[v]) { int id = g[v][ptr[v]], to = e[id].b; if (d[to] != d[v] + 1) continue; int pushed = dfs (to, min (flow, e[id].cap - e[id].flow)); if (pushed) { e[id].flow += pushed; e[id^1].flow -= pushed; return pushed; } } return 0; } int dinic() { int flow = 0; for (;;) { if (!bfs()) break; memset (ptr, 0, n * sizeof ptr[0]); while (int pushed = dfs (s, INF)) flow += pushed; } return flow; }
Сеть должна быть предварительно считана: должны быть заданы переменные  ,
,  ,
,  , а также добавлены все рёбра (ориентированные) с помощью вызовов функции
, а также добавлены все рёбра (ориентированные) с помощью вызовов функции 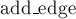 . Основная функция решения —
. Основная функция решения — 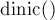 , которая возвращает величину найденного максимального потока.
, которая возвращает величину найденного максимального потока.