Модульное линейное уравнение первого порядка

Постановка задачи

Это уравнение вида:

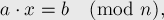
$a \cdot x = b \pmod n,$

где 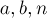$a, b, n$ — заданные целые числа, $x$ — неизвестное целое число.

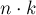Требуется найти искомое значение $x$ , лежащее в отрезке $[0; n-1]$ (поскольку на всей числовой прямой, ясно, может существовать бесконечно много решений, которые будут отличаться друг друга на $n \cdot k$ , где $k$ — любое целое число). Если решение не единственно, то мы рассмотрим, как получить все решения.

Решение с помощью нахождения Обратного элемента

Рассмотрим сначала более простой случай — когда $a$ и $n$ взаимно просты. Тогда можно найти обратный элемент к числу $a$ , и, домножив на него обе части уравнения, получить решение (и оно будет единственным):

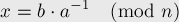
$x = b \cdot a^{-1} \pmod n$

Теперь рассмотрим случай, когда $a$ и $n$ не взаимно просты. Тогда, очевидно, решение будет существовать не всегда (например, $2 \cdot x = 1 \pmod 4$ ).

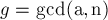Пусть $g = {\rm gcd(a,n)}$ , т.е. их наибольший общий делитель (который в данном случае больше единицы).

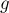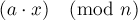Тогда, если $b$ не делится на $g$ , то решения не существует. В самом деле, при любом $x$ левая часть уравнения, т.е. $(a \cdot x) \pmod n$ , всегда делится на 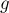$g$ , в то время как правая часть на него не делится, откуда и следует, что решений нет.

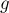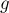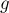Если же $b$ делится на $g$ , то, разделив обе части уравнения на это $g$ (т.е. разделив $a$ , $b$ и $n$ на $g$ ), мы придём к новому уравнению:

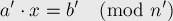
$a^\prime \cdot x = b^\prime \pmod {n^\prime}$

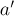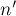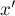в котором $a^\prime$ и $n^\prime$ уже будут взаимно просты, а такое уравнение мы уже научились решать. Обозначим его решение через $x^\prime$ .

Понятно, что это 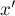$x^\prime$ будет также являться и решением исходного уравнения. Однако если 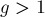$g > 1$ , то оно будет не единственным решением. Можно показать, что исходное уравнение будет иметь ровно 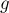$g$ решений, и они будут иметь вид:

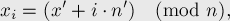
$x_i = (x^\prime + i \cdot n^\prime) \pmod n,$
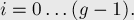
$i = 0 \ldots (g-1).$

Подводя итог, можно сказать, что количество решений линейного модульного уравнения равно либо 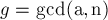$g = {\rm gcd(a,n)}$ , либо нулю.

Решение с помощью Расширенного алгоритма Евклида

Приведём наше модулярное уравнение к диофантову уравнению следующим образом:

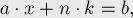
$a \cdot x + n \cdot k = b,$

где $x$ и $k$ — неизвестные целые числа.

Способ решения этого уравнения описан в соответствующей статье Линейные диофантовы уравнения второго порядка, и заключается он в применении Расширенного алгоритма Евклида.

Там же описан и способ получения всех решений этого уравнения по одному найденному решению, и, кстати говоря, этот способ при внимательном рассмотрении абсолютно эквивалентен способу, описанному в предыдущем пункте.