MAXimal
добавлено: 11 Jul 2008 13:58
редактировано: 27 May 2012 17:55
Содержание [скрыть]
Нахождение степени делителя факториала
Даны два числа:  и
и  . Требуется посчитать, с какой степенью делитель
. Требуется посчитать, с какой степенью делитель  входит в число
входит в число 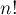 , т.е. найти наибольшее
, т.е. найти наибольшее  такое, что
такое, что 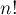 делится на
делится на 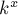 .
.
Решение для случая простого 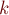
Рассмотрим сначала случай, когда  простое.
простое.
Выпишем выражение для факториала в явном виде:
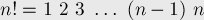
Заметим, что каждый  -ый член этого произведения делится на
-ый член этого произведения делится на  , т.е. даёт +1 к ответу; количество таких членов равно
, т.е. даёт +1 к ответу; количество таких членов равно 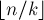 .
.
Далее, заметим, что каждый 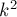 -ый член этого ряда делится на
-ый член этого ряда делится на 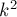 , т.е. даёт ещё +1 к ответу (учитывая, что
, т.е. даёт ещё +1 к ответу (учитывая, что  в первой степени уже было учтено до этого); количество таких членов равно
в первой степени уже было учтено до этого); количество таких членов равно 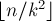 .
.
И так далее, каждый 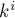 -ый член ряда даёт +1 к ответу, а количество таких членов равно
-ый член ряда даёт +1 к ответу, а количество таких членов равно 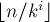 .
.
Таким образом, ответ равен величине:
![\frac{n}{k} + \frac{n}{k^2} + \ldots + \frac{n}{k[...]](../tex2png/cache/937f7e1100fb720eb0a2f22ef574eabb.png)
Эта сумма, разумеется, не бесконечная, т.к. только первые примерно 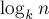 членов отличны от нуля. Следовательно, асимптотика такого алгоритма равна
членов отличны от нуля. Следовательно, асимптотика такого алгоритма равна 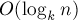 .
.
Реализация:
int fact_pow (int n, int k) { int res = 0; while (n) { n /= k; res += n; } return res; }
Решение для случая составного 
Ту же идею применить здесь непосредственно уже нельзя.
Но мы можем факторизовать  , решить задачу для каждого его простого делителя, а потом выбрать минимум из ответов.
, решить задачу для каждого его простого делителя, а потом выбрать минимум из ответов.
Более формально, пусть 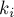 — это
— это  -ый делитель числа
-ый делитель числа  , входящий в него в степени
, входящий в него в степени 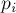 . Решим задачу для
. Решим задачу для 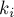 с помощью вышеописанной формулы за
с помощью вышеописанной формулы за 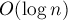 ; пусть мы получили ответ
; пусть мы получили ответ 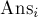 . Тогда ответом для составного
. Тогда ответом для составного  будет минимум из величин
будет минимум из величин 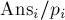 .
.
Учитывая, что факторизация простейшим образом выполняется за 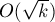 , получаем итоговую асимптотику
, получаем итоговую асимптотику 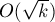 .
.