MAXimal
добавлено: 6 Sep 2011 1:03
редактировано: 16 Nov 2011 23:48
Содержание [скрыть]
Heavy-light декомпозиция
Heavy-light декомпозиция — это достаточно общий приём, который позволяет эффективно решать многие задачи, сводящиеся к запросам на дереве.
Простейший пример задач такого вида — это следующая задача. Дано дерево, каждой вершине которого приписано какое-то число. Поступают запросы вида 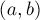 , где
, где  и
и  — номера вершин дерева, и требуется узнать максимальное число на пути между вершинами
— номера вершин дерева, и требуется узнать максимальное число на пути между вершинами  и
и  .
.
Описание алгоритма
Итак, пусть дано дерево 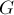 с
с  вершинами, подвешенное за некоторый корень.
вершинами, подвешенное за некоторый корень.
Суть этой декомпозиции в том, чтобы разбить дерево на несколько путей таким образом, чтобы для любой вершины  получалось, что если мы будем подниматься от
получалось, что если мы будем подниматься от  к корню, то по пути сменим не более
к корню, то по пути сменим не более 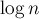 путей. Кроме того, все пути должны не пересекаться друг с другом по рёбрам.
путей. Кроме того, все пути должны не пересекаться друг с другом по рёбрам.
Понятно, что если мы научимся искать такую декомпозицию для любого дерева, это позволит свести любой запрос вида "узнать что-то на пути из  в
в  " к нескольким запросам вида "узнать что-то на отрезке
" к нескольким запросам вида "узнать что-то на отрезке ![[l;r]](../tex2png/cache/26853b907ea3f6227b00c5afac10292a.png)
 -го пути".
-го пути".
Построение heavy-light декомпозиции
Посчитаем для каждой вершины  размер её поддерева
размер её поддерева 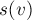 (т.е. это количество вершин в поддереве вершины
(т.е. это количество вершин в поддереве вершины  , включая саму вершину).
, включая саму вершину).
Далее, рассмотрим все рёбра, ведущие к сыновьям какой-либо вершины  . Назовём ребро
. Назовём ребро 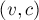 тяжёлым, если оно ведёт в вершину
тяжёлым, если оно ведёт в вершину  такую, что:
такую, что:
![s(c) \ge \frac{ s(v) }{ 2 } ~~~~ \Leftrightarrow [...]](../tex2png/cache/7e1adc211a0cf920b1dbc0cb461809ca.png)
Все остальные рёбра назовём лёгкими. Очевидно, что из одной вершины  вниз может исходить максимум одно тяжёлое ребро (т.к. в противном случае у вершины
вниз может исходить максимум одно тяжёлое ребро (т.к. в противном случае у вершины  было бы два сына размера
было бы два сына размера 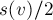 , что с учётом самой вершины
, что с учётом самой вершины  даёт размер
даёт размер 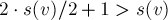 , т.е. пришли к противоречию).
, т.е. пришли к противоречию).
Теперь построим саму декомпозицию дерева на непересекающиеся пути. Рассмотрим все вершины, из которых не выходит вниз ни одного тяжёлого ребра, и будем идти от каждой из них вверх, пока не дойдём до корня дерева или не пройдём лёгкое ребро. В результате мы получим несколько путей — покажем, что это и есть искомые пути heavy-light декомпозиции.
Доказательство корректности алгоритма
Во-первых, заметим, что полученные алгоритмом пути будут непересекающимися. В самом деле, если бы два каких-то пути имели бы общее ребро, это бы означало, что из какой-то вершины исходит вниз два тяжёлых ребра, чего быть не может.
Во-вторых, покажем, что спускаясь от корня дерева до произвольной вершины, мы сменим по пути не более 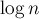 путей. В самом деле, проход вниз по лёгкому ребру уменьшает размер текущего поддерева более чем вдвое:
путей. В самом деле, проход вниз по лёгкому ребру уменьшает размер текущего поддерева более чем вдвое:
![s(c) < \frac{ s(v) }{ 2 } ~~~~ \Leftrightarrow ~~[...]](../tex2png/cache/7a8de12630f4130b1c0a95a6aa7dfbe5.png)
Таким образом, мы не могли пройти более 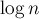 лёгких рёбер. Однако переходить с одного пути на другой мы можем только через лёгкое ребро (т.к. каждый путь, кроме заканчивающихся в корне, содержит лёгкое ребро в конце; а попасть сразу посередине пути мы не можем).
лёгких рёбер. Однако переходить с одного пути на другой мы можем только через лёгкое ребро (т.к. каждый путь, кроме заканчивающихся в корне, содержит лёгкое ребро в конце; а попасть сразу посередине пути мы не можем).
Следовательно, по пути от корня до любой вершины мы не можем сменить более 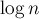 путей, что и требовалось доказать.
путей, что и требовалось доказать.
Применения при решении задач
При решении задач иногда бывает удобнее рассматривать heavy-light как набор вершинно-непересекающихся путей (а не рёберо-непересекающихся). Для этого достаточно из каждого пути исключить последнее ребро, если оно являются лёгким ребром — тогда никакие свойства не нарушатся, но теперь каждая вершина будет принадлежать ровно одному пути.
Ниже мы рассмотрим несколько типичных задач, которые можно решать с помощью heavy-light декомпозиции.
Отдельно стоит обратить внимание на задачу сумма чисел на пути, поскольку это пример задачи, которая может быть решена и более простыми техниками.
Максимальное число на пути между двумя вершинами
Дано дерево, каждой вершине которого приписано какое-то число. Поступают запросы вида 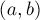 , где
, где  и
и  — номера вершин дерева, и требуется узнать максимальное число на пути между вершинами
— номера вершин дерева, и требуется узнать максимальное число на пути между вершинами  и
и  .
.
Построим заранее heavy-light декомпозицию. Над каждым получившимся путём построим дерево отрезков для максимума, что позволит искать вершину с максимальным приписанным числом в указанном сегменте указанного пути за 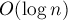 . Хотя число путей в heavy-light декомпозиции может достигать
. Хотя число путей в heavy-light декомпозиции может достигать 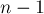 , суммарный размер всех путей есть величина
, суммарный размер всех путей есть величина  , поэтому и суммарный размер деревьев отрезков также будет линейным.
, поэтому и суммарный размер деревьев отрезков также будет линейным.
Теперь, для того чтобы отвечать на поступивший запрос 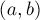 найдём наименьшего общего предка
найдём наименьшего общего предка 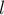 этих вершин (например, методом двоичного подъёма). Теперь задача свелась к двум запросам:
этих вершин (например, методом двоичного подъёма). Теперь задача свелась к двум запросам: 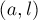 и
и 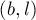 , на каждый из которых мы можем ответить таким образом: найдём, в каком пути лежит нижняя вершина, сделаем запрос к этому пути, перейдём в вершину-конец этого пути, снова определим, в каком мы пути оказались и сделаем запрос к нему, и так далее, пока не дойдём до пути, содержащего
, на каждый из которых мы можем ответить таким образом: найдём, в каком пути лежит нижняя вершина, сделаем запрос к этому пути, перейдём в вершину-конец этого пути, снова определим, в каком мы пути оказались и сделаем запрос к нему, и так далее, пока не дойдём до пути, содержащего 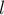 .
.
Аккуратно следует быть со случаем, когда, например,  и
и 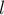 оказались в одном пути — тогда запрос максимума к этому пути надо делать не на суффиксе, а на внутреннем подотрезке.
оказались в одном пути — тогда запрос максимума к этому пути надо делать не на суффиксе, а на внутреннем подотрезке.
Таким образом, в процессе ответа на один подзапрос мы пройдём по 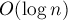 путям, в каждом из них сделав запрос максимума на суффиксе или на префиксе/подотрезке (запрос на префиксе/подотрезке мог быть только один раз).
путям, в каждом из них сделав запрос максимума на суффиксе или на префиксе/подотрезке (запрос на префиксе/подотрезке мог быть только один раз).
Так мы получили решение за 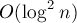 на один запрос.
на один запрос.
Если ещё дополнительно предпосчитать на каждом пути максимумы на всех суффиксах, то получится решение за 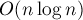 — т.к. запрос максимума не на суффиксе случается только один раз, когда мы доходим до вершины
— т.к. запрос максимума не на суффиксе случается только один раз, когда мы доходим до вершины 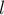 .
.
Сумма чисел на пути между двумя вершинами
Дано дерево, каждой вершине которого приписано какое-то число. Поступают запросы вида 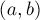 , где
, где  и
и  — номера вершин дерева, и требуется узнать сумму чисел на пути между вершинами
— номера вершин дерева, и требуется узнать сумму чисел на пути между вершинами  и
и  . Возможен вариант этой задачи, когда дополнительно бывают запросы изменения числа, приписанного той или иной вершине.
. Возможен вариант этой задачи, когда дополнительно бывают запросы изменения числа, приписанного той или иной вершине.
Хотя эту задачу можно решать с помощью heavy-light декомпозиции, построив над каждым путём дерево отрезков для суммы (или просто предпосчитав частичные суммы, если в задаче отсутствуют запросы изменения), эта задача может быть решена более простыми техниками.
Если запросы модификации отсутствуют, то узнавать сумму на пути между двумя вершинами можно параллельно с поиском LCA двух вершин в алгоритме двоичного подъёма — для этого достаточно во время препроцессинга для LCA подсчитывать не только 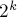 -ых предков каждой вершины, но и сумму чисел на пути до этого предка.
-ых предков каждой вершины, но и сумму чисел на пути до этого предка.
Есть и принципиально другой подход к этой задаче — рассмотреть эйлеров обход дерева, и построить дерево отрезков над ним. Этот алгоритм рассматривается в статье с решением похожей задачи. (А если запросы модификации отсутствуют — то достаточно обойтись предпосчётом частичных сумм, без дерева отрезков.)
Оба этих способа дают относительно простые решения с асимптотикой 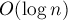 на один запрос.
на один запрос.
Перекраска рёбер пути между двумя вершинами
Дано дерево, каждое ребро изначально покрашено в белый цвет. Поступают запросы вида 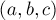 , где
, где  и
и  — номера вершин,
— номера вершин,  — цвет, что означает, что все рёбра на пути из
— цвет, что означает, что все рёбра на пути из  в
в  надо перекрасить в цвет
надо перекрасить в цвет  . Требуется после всех перекрашиваний сообщить, сколько в итоге получилось рёбер каждого цвета.
. Требуется после всех перекрашиваний сообщить, сколько в итоге получилось рёбер каждого цвета.
Решение — просто сделать дерево отрезков с покраской на отрезке над набором путей heavy-light декомпозиции.
Каждый запрос перекраски на пути 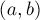 превратится в два подзапроса
превратится в два подзапроса 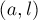 и
и 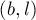 , где
, где 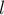 — наименьший общий предок вершин
— наименьший общий предок вершин  и
и  (найденный, например, алгоритмом двоичного подъёма), а каждый из этих подзапросов — в
(найденный, например, алгоритмом двоичного подъёма), а каждый из этих подзапросов — в 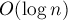 запросов к деревьям отрезков над путями.
запросов к деревьям отрезков над путями.
Итого получается решение с асимптотикой 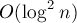 на один запрос.
на один запрос.
Задачи в online judges
Список задач, которые можно решить, используя heavy-light декомпозицию:
- TIMUS #1553 "Caves and Tunnels" [сложность: средняя]
- IPSC 2009 L "Let there be rainbows!" [сложность: средняя]
- SPOJ #2798 "Query on a tree again!" [сложность: средняя]
- Codeforces Beta Round #88 E "Дерево или не дерево" [сложность: высокая]