Нахождение вписанной окружности в выпуклом многоугольнике методом "сжатия сторон" ("shrinking sides") за 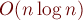$O (n \log n)$

Дан выпуклый многоугольник с $n$ вершинами. Требуется найти вписанную в него окружность максимального радиуса: т.е. найти её радиус и координаты центра. (Если при данном радиусе возможны несколько вариантов центров, то достаточно найти любой из них.)

В отличие от описанного здесь метода двойного тернарного поиска, асимптотика данного алгоритма — 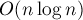$O (n \log n)$ — не зависит от ограничений на координаты и от требуемой точности, и поэтому этот алгоритм подходит при значительно больших $n$ и больших ограничениях на величину координат.

Спасибо Ивану Красильникову (mf) за описание этого красивого алгоритма.

Алгоритм

Итак, дан выпуклый многоугольник. Начнём одновременно и с одинаковой скоростью сдвигать все его стороны параллельно самим себе внутрь многоугольника:

Пусть, для удобства, это движение происходит со скоростью 1 координатная единица в секунду (т.е. время в каком-то смысле равно расстоянию: спустя единицу времени каждая точка преодолеет расстояние, равное единице).

В процессе этого движения стороны многоугольника будут постепенно исчезать (обращаться в точки). Рано или поздно весь многоугольник сожмётся в точку или отрезок, и этот момент времени $t$ будет являться ответом на задачу — искомым радиусом (а центр искомой окружности будет лежать на этом отрезке). В самом деле, если мы сжали многоугольник на толщину $t$ по всем направлениям, и он обратился в точку/отрезок, то это означает, что существует точка, отстоящая от всех сторон многоугольника на расстоянии $t$ , а для бОльших расстояний — такой точки уже не существует.

Итак, нам надо научиться эффективно моделировать этот процесс сжатия. Для этого научимся для каждой стороны определять время, через которое она сожмётся в точку.

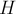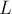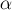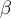Для этого рассмотрим внимательно процесс движения сторон. Заметим, что вершины многоугольника всегда движутся по биссектрисам углов (это следует из равенства соответствующих треугольников). Но тогда вопрос о времени, через которое сторона сожмётся, сводится к вопросу об определении высоты $H$ треугольника, в котором известна длина стороны $L$ и два прилежащих к ней угла $\alpha$ и $\beta$ . Воспользовавшись, например, теоремой синусов, получаем формулу:

$H = L \cdot \frac{ \sin \alpha \cdot \sin \beta }[...]$

Теперь мы умеем за 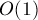$O(1)$ определять время, через которое сторона сожмётся в точку.

Занесём эти времена для каждой стороны в некую структуру данных для извлечения минимума, например, красно-чёрное дерево (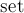 $\rm set$ в языке C++).

Теперь если мы извлечём сторону с наименьшим временем 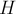$H$ , то эта сторона первой сожмётся в точку — в момент времени 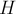$H$ . Если многоугольник ещё не сжался в точку/отрезок, то эту сторону надо удалить из многоугольника, и продолжить алгоритм для оставшихся сторон. При удалении стороны мы должны соединить друг с другом её левого и правого соседа, продлив их до точки их пересечения. При этом необходимо будет найти эту точку пересечения, пересчитать длины двух сторон и их времена исчезновения.

При реализации для каждой стороны придётся хранить номер её правого и левого соседа (тем самым как бы построив двусвязный список из сторон многоугольника). Это позволяет реализовать удаление стороны и связывание двух её соседей за 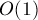$O(1)$ .

Если при удалении стороны оказывается, что её стороны-соседи параллельны, то это означает, что многоугольник после этого сжатия вырождается в точку/отрезок, поэтому мы можем сразу останавливать алгоритм и возвращать в качестве ответа время исчезнования текущей стороны (так что проблем с параллельными сторонами не возникает).

Если же такая ситуация с параллельными сторонами не возникает, то алгоритм доработает до момента, в который в многоугольнике останется только две стороны — и тогда ответом на задачу будет являться время удаления предыдущей стороны.

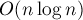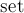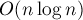Очевидно, асимптотика этого алгоритма составляет $O (n \log n)$ , поскольку алгоритм состоит из $n$ шагов, на каждом из которых удаляется по одной стороне (для чего производится несколько операций с $\rm set$ за время $O (n \log n)$ ).

Реализация

Приведём реализацию описанного выше алгоритма. Данная реализация возвращает только радиус искомой окружности; впрочем, добавление вывода центра окружности не составит большого труда.

Данный алгоритм элегантен тем, что из вычислительной геометрии требуется только нахождение угла между двумя сторонами, пересечение двух прямых и проверка двух прямых на параллельность.

Примечание. Предполагается, что подаваемый на вход многоугольник — строго выпуклый, т.е. никакие три точки не лежат на одной прямой.

const double EPS = 1E-9;
const double PI = ...;
 
struct pt {
	double x, y;
	pt()  { }
	pt (double x, double y) : x(x), y(y)  { }
	pt operator- (const pt & p) const {
		return pt (x-p.x, y-p.y);
	}
};
 
double dist (const pt & a, const pt & b) {
	return sqrt ((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
 
double get_ang (const pt & a, const pt & b) {
	double ang = abs (atan2 (a.y, a.x) - atan2 (b.y, b.x));
	return min (ang, 2*PI-ang);
}
 
struct line {
	double a, b, c;
	line (const pt & p, const pt & q) {
		a = p.y - q.y;
		b = q.x - p.x;
		c = - a * p.x - b * p.y;
		double z = sqrt (a*a + b*b);
		a/=z, b/=z, c/=z;
	}
};
 
double det (double a, double b, double c, double d) {
	return a * d - b * c;
}
 
pt intersect (const line & n, const line & m) {
	double zn = det (n.a, n.b, m.a, m.b);
	return pt (
		- det (n.c, n.b, m.c, m.b) / zn,
		- det (n.a, n.c, m.a, m.c) / zn
	);
}
 
bool parallel (const line & n, const line & m) {
	return abs (det (n.a, n.b, m.a, m.b)) < EPS;
}
 
double get_h (const pt & p1, const pt & p2,
	const pt & l1, const pt & l2, const pt & r1, const pt & r2)
{
	pt q1 = intersect (line (p1, p2), line (l1, l2));
	pt q2 = intersect (line (p1, p2), line (r1, r2));
	double l = dist (q1, q2);
	double alpha = get_ang (l2 - l1, p2 - p1) / 2;
	double beta = get_ang (r2 - r1, p1 - p2) / 2;
	return l * sin(alpha) * sin(beta) / sin(alpha+beta);
}
 
struct cmp {
	bool operator() (const pair<double,int> & a, const pair<double,int> & b) const {
		if (abs (a.first - b.first) > EPS)
			return a.first < b.first;
		return a.second < b.second;
	}
};
 
int main() {
	int n;
	vector<pt> p;
	... чтение n и p ...
 
	vector<int> next (n), prev (n);
	for (int i=0; i<n; ++i) {
		next[i] = (i + 1) % n;
		prev[i] = (i - 1 + n) % n;
	}
 
	set < pair<double,int>, cmp > q;
	vector<double> h (n);
	for (int i=0; i<n; ++i) {
		h[i] = get_h (
			p[i], p[next[i]],
			p[i], p[prev[i]],
			p[next[i]], p[next[next[i]]]
		);
		q.insert (make_pair (h[i], i));
	}
 
	double last_time;
	while (q.size() > 2) {
		last_time = q.begin()->first;
		int i = q.begin()->second;
		q.erase (q.begin());
 
		next[prev[i]] = next[i];
		prev[next[i]] = prev[i];
		int nxt = next[i],   nxt1 = (nxt+1)%n,
			prv = prev[i],   prv1 = (prv+1)%n;
		if (parallel (line (p[nxt], p[nxt1]), line (p[prv], p[prv1])))
			break;
 
		q.erase (make_pair (h[nxt], nxt));
		q.erase (make_pair (h[prv], prv));
 
		h[nxt] = get_h (
			p[nxt], p[nxt1],
			p[prv1], p[prv],
			p[next[nxt]], p[(next[nxt]+1)%n]
		);
		h[prv] = get_h (
			p[prv], p[prv1],
			p[(prev[prv]+1)%n], p[prev[prv]],
			p[nxt], p[nxt1]
		);
 
		q.insert (make_pair (h[nxt], nxt));
		q.insert (make_pair (h[prv], prv));
	}
 
	cout << last_time << endl;
}

Основная функция здесь — это 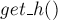$get\_h()$ , которая по стороне и её левому и правому соседям вычисляет время исчезновения этой стороны. Для этого ищется точка пересечения этой стороны с соседями, и затем по приведённой выше формуле производится рассчёт искомого времени.