MAXimal
добавлено: 11 Jun 2008 11:20
редактировано: 2 Dec 2010 10:29
Содержание [скрыть]
Задача Джонсона с одним станком
Это задача составления оптимального расписания обработки  деталей на единственном станке, если
деталей на единственном станке, если  -ая деталь обрабатывается на нём за время
-ая деталь обрабатывается на нём за время 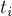 , а за
, а за  секунд ожидания до обработки этой детали платится штраф
секунд ожидания до обработки этой детали платится штраф 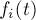 .
.
Таким образом, задача заключается в поиске такого переупорядочения деталей, что следующая величина (размер штрафа) минимальна. Если мы обозначим через 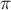 перестановку деталей (
перестановку деталей (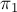 — номер первой обрабатываемой детали,
— номер первой обрабатываемой детали, 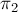 — второй, и т.д.), то размер штрафа
— второй, и т.д.), то размер штрафа 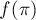 равен:
равен:
![F(\pi) = f_{\pi_1}(0) + f_{\pi_2}(t_{\pi_1}) + f_[...]](../tex2png/cache/16621ab5d3e8a54f7edbe360e95c5287.png)
Иногда эта задача называется задачей однопроцессорного обслуживания множества заявок.
Решение задачи в некоторых частных случаях
Первый частный случай: линейные функции штрафа
Научимся решать эту задачу в случае, когда все 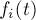 линейны, т.е. имеют вид:
линейны, т.е. имеют вид:
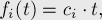
где 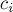 — неотрицательные числа. Заметим, что в этих линейных функциях свободный член равен нулю, т.к. в противном случае к ответу сразу можно прибавить этот свободный член, и решать задачу с нулевым свободным членом.
— неотрицательные числа. Заметим, что в этих линейных функциях свободный член равен нулю, т.к. в противном случае к ответу сразу можно прибавить этот свободный член, и решать задачу с нулевым свободным членом.
Зафиксируем некоторое расписание — перестановку 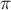 . Зафиксируем какой-то номер
. Зафиксируем какой-то номер 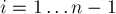 , и пусть перестановка
, и пусть перестановка 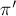 равна перестановке
равна перестановке 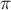 , в которой обменяли
, в которой обменяли  -ый и
-ый и 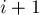 -ый элементы. Посмотрим, на сколько при этом изменился штраф:
-ый элементы. Посмотрим, на сколько при этом изменился штраф:
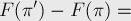
легко понять, что изменения произошли только с  -ым и
-ым и 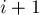 -ым слагаемыми:
-ым слагаемыми:
![= c_{\pi^\prime_i} \cdot \sum_{k=1}^{i-1} t_{\pi^[...]](../tex2png/cache/0bbf10c5349d79fd3c4b25bb443361c2.png)
![= c_{\pi_{i+1}} \cdot \sum_{k=1}^{i-1} t_{\pi^\pr[...]](../tex2png/cache/4b49dc0d10ae824051d9ee9f411ff11e.png)
![= c_{\pi_i} \cdot t_{\pi_{i+1}} - c_{\pi_{i+1}} \[...]](../tex2png/cache/bf3ee8296e0c8d3c78e7d363b683a67f.png)
Понятно, что если расписание 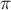 является оптимальным, то любое его изменение приводит к увеличению штрафа (или сохранению прежнего значения), поэтому для оптимального плана можно записать условие:
является оптимальным, то любое его изменение приводит к увеличению штрафа (или сохранению прежнего значения), поэтому для оптимального плана можно записать условие:
![\forall i=1 \ldots n-1 ~~~:~~ c_{\pi_i} \cdot t_{[...]](../tex2png/cache/183d0fbcf0544ecde073fd28af07e8f2.png)
Преобразуя, получаем:
![\forall i=1 \ldots n-1 ~~~:~~ \frac{ c_{\pi_i} }{[...]](../tex2png/cache/16d59c4ca880fd8836e2be48a1a90942.png)
Таким образом, оптимальное расписание можно получить, просто отсортировав все детали по отношению 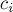 к
к 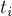 в обратном порядке.
в обратном порядке.
Следует отметить, что мы получили этот алгоритм так называемым перестановочным приёмом: мы попробовали обменять местами два соседних элемента расписания, вычислили, насколько при этом изменился штраф, и отсюда вывели алгоритм поиска оптимального расписания.
Второй частный случай: экспоненциальные функции штрафа
Пусть теперь функции штрафа имеют вид:
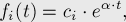
где все числа 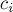 неотрицательны, константа
неотрицательны, константа 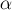 положительна.
положительна.
Тогда, применяя аналогичным образом здесь перестановочный приём, легко получить, что детали надо сортировать в порядке убывания величин:
![v_i = \frac{ 1 - e^{ \alpha \cdot t_i } }{ c_i }.[...]](../tex2png/cache/ea8246b1a516b291290901ffc4541c4e.png)
Третий частный случай: одинаковые монотонные функции штрафа
В этом случае считается, что все 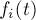 совпадают с некоторой функцией
совпадают с некоторой функцией 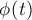 , которая является возрастающей.
, которая является возрастающей.
Понятно, что в этом случае оптимально располагать детали в порядке увеличения времени обработки 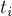 .
.
Теорема Лившица-Кладова
Теорема Лившица-Кладова устанавливает, что перестановочный приём применим только для вышеописанных трёх частных случаев, и только них, т.е.:
- Линейный случай:
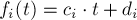 , где
, где 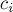 — неотрицательные константы,
— неотрицательные константы, - Экспоненциальный случай:
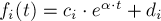 , где
, где 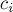 и
и 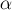 — положительные константы,
— положительные константы, - Тождественный случай:
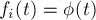 , где
, где 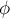 — возрастающая функция.
— возрастающая функция.
Эта теорема доказана в предположении, что функции штрафа являются достаточно гладкими (существуют третьи производные).
Во всех трёх случаях применим перестановочный приём, благодаря которому искомое оптимальное расписание может быть найдено простой сортировкой, следовательно, за время 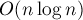 .
.