MAXimal
добавлено: 11 Jun 2008 11:25
редактировано: 14 Oct 2011 0:05
Содержание [скрыть]
Задача Иосифа
Условие задачи. Даны натуральные  и
и  . По кругу выписывают все натуральные числа от 1 до
. По кругу выписывают все натуральные числа от 1 до  . Сначала отсчитывают
. Сначала отсчитывают  -ое число, начиная с первого, и удаляют его. Затем от него отсчитывают
-ое число, начиная с первого, и удаляют его. Затем от него отсчитывают  чисел и
чисел и  -ое удаляют, и т.д. Процесс останавливается, когда остаётся одно число. Требуется найти это число.
-ое удаляют, и т.д. Процесс останавливается, когда остаётся одно число. Требуется найти это число.
Задача была поставлена Иосифом Флавием (Flavius Josephus) ещё в 1 веке (правда, в несколько более узкой формулировке: при 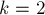 ).
).
Решать эту задачу можно моделированием. Простейшее моделирование будет работать 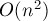 . Используя Дерево отрезков, можно произвести моделирование за
. Используя Дерево отрезков, можно произвести моделирование за 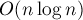 .
.
Решение за 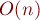
Попытаемся найти закономерность, выражающую ответ для задачи 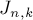 через решение предыдущих задач.
через решение предыдущих задач.
С помощью моделирования построим таблицу значений, например, такую:
![\bordermatrix {
n \setminus k&1&2&3&4&5&6&7&8&9&[...]](../tex2png/cache/7c22e1659a058076cce91fcb77486072.png)
И здесь достаточно отчётливо видна следующая закономерность:
![J_{n,k} = \left( J_{(n-1),k} + k - 1 \right)\ \%\[...]](../tex2png/cache/80f20fb43ce2018e670d4afbcbaa1287.png)
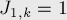
Здесь 1-индексация несколько портит элегантность формулы, если нумеровать позиции с нуля, то получится очень наглядная формула:
![J_{n,k} = \left( J_{(n-1),k} + k \right)\ \%\ n =[...]](../tex2png/cache/e31a6a8b1c05ac13b5d741e210236b2a.png)
Итак, мы нашли решение задачи Иосифа, работающее за 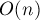 операций.
операций.
Простая рекурсивная реализация (в 1-индексации):
int joseph (int n, int k) { return n>1 ? (joseph (n-1, k) + k - 1) % n + 1 : 1; }
Нерекурсивная форма:
int joseph (int n, int k) { int res = 0; for (int i=1; i<=n; ++i) res = (res + k) % i; return res + 1; }
Решение за 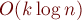
Для сравнительно небольших  можно придумать более оптимальное решение, чем рассмотренное выше рекурсивное решение за
можно придумать более оптимальное решение, чем рассмотренное выше рекурсивное решение за  . Если
. Если  небольшое, то даже интуитивно понятно, что тот алгоритм делает много лишних действий: серьёзные изменения происходят, только когда происходит взятие по модулю
небольшое, то даже интуитивно понятно, что тот алгоритм делает много лишних действий: серьёзные изменения происходят, только когда происходит взятие по модулю  , а до этого момента алгоритм просто несколько раз прибавляет к ответу число
, а до этого момента алгоритм просто несколько раз прибавляет к ответу число  . Соответственно, можно избавиться от этих ненужных шагов,
. Соответственно, можно избавиться от этих ненужных шагов,
Небольшая возникающая при этом сложность заключается в том, что после удаления этих чисел у нас получится задача с меньшим  , но стартовой позицией не в первом числе, а где-то в другом месте. Поэтому, вызвав рекурсивно себя от задачи с новым
, но стартовой позицией не в первом числе, а где-то в другом месте. Поэтому, вызвав рекурсивно себя от задачи с новым  , мы затем должны аккуратно перевести результат в нашу систему нумерации из его собственной.
, мы затем должны аккуратно перевести результат в нашу систему нумерации из его собственной.
Также отдельно надо разбирать случай, когда  станет меньше
станет меньше  — в этом случае вышеописанная оптимизация выродится в бесконечный цикл.
— в этом случае вышеописанная оптимизация выродится в бесконечный цикл.
Реализация (для удобства в 0-индексации):
int joseph (int n, int k) { if (n == 1) return 0; if (k == 1) return n-1; if (k > n) return (joseph (n-1, k) + k) % n; int cnt = n / k; int res = joseph (n - cnt, k); res -= n % k; if (res < 0) res += n; else res += res / (k - 1); return res; }
Оценим асимптотику этого алгоритма. Сразу заметим, что случай 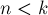 разбирается у нас старым решением, которое отработает в данном случае за
разбирается у нас старым решением, которое отработает в данном случае за 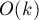 . Теперь рассмотрим сам алгоритм. Фактически, на каждой его итерации вместо
. Теперь рассмотрим сам алгоритм. Фактически, на каждой его итерации вместо  чисел мы получаем примерно
чисел мы получаем примерно 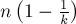 чисел, поэтому общее число
чисел, поэтому общее число  итераций алгоритма примерно можно найти из уравнения:
итераций алгоритма примерно можно найти из уравнения:
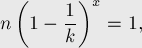
![\ln n + x \ln \left( 1 - \frac{1}{k} \right) = 0,[...]](../tex2png/cache/f57e1efa9a9e8052c80af1215ad953f8.png)
![x = - \frac{ \ln n }{ \ln \left( 1 - \frac{1}{k} [...]](../tex2png/cache/e06de24bbc9d5de1a2c44554f7b48093.png)
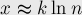
Таким образом, асимптотика алгоритма действительно 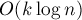 .
.
Аналитическое решение для 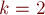
В этом частном случае (в котором и была поставлена эта задача Иосифом Флавием) задача решается значительно проще.
В случае чётного  получаем, что будут вычеркнуты все чётные числа, а потом останется задача для
получаем, что будут вычеркнуты все чётные числа, а потом останется задача для 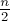 , тогда ответ для
, тогда ответ для  будет получаться из ответа для
будет получаться из ответа для 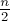 умножением на два и вычитанием единицы (за счёт сдвига позиций):
умножением на два и вычитанием единицы (за счёт сдвига позиций):
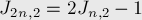
Аналогично, в случае нечётного  будут вычеркнуты все чётные числа, затем первое число, и останется задача для
будут вычеркнуты все чётные числа, затем первое число, и останется задача для 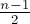 , и с учётом сдвига позиций получаем вторую формулу:
, и с учётом сдвига позиций получаем вторую формулу:
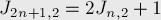
При реализации можно непосредственно использовать эту рекуррентную зависимость. Можно эту закономерность перевести в другую форму: 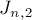 представляют собой последовательность всех нечётных чисел, "перезапускающуюся" с единицы всякий раз, когда
представляют собой последовательность всех нечётных чисел, "перезапускающуюся" с единицы всякий раз, когда  оказывается степенью двойки. Это можно записать и в виде одной формулы:
оказывается степенью двойки. Это можно записать и в виде одной формулы:
![J_{n,2} = 1 + 2 \left( n - 2^{\lfloor \log_2 n \r[...]](../tex2png/cache/a262aa4ea1e0e2967300fe22a307981c.png)
Аналитическое решение для 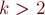
Несмотря на простой вид задачи и большое количество статей по этой и смежным задачам, простого аналитического представления решения задачи Иосифа до сих пор не найдено. Для небольших  выведены некоторые формулы, но, по-видимому, все они трудноприменимы на практике (например, см. Halbeisen, Hungerbuhler "The Josephus Problem" и Odlyzko, Wilf "Functional iteration and the Josephus problem").
выведены некоторые формулы, но, по-видимому, все они трудноприменимы на практике (например, см. Halbeisen, Hungerbuhler "The Josephus Problem" и Odlyzko, Wilf "Functional iteration and the Josephus problem").