MAXimal
добавлено: 11 Jun 2008 11:09
редактировано: 24 Oct 2010 23:40
Содержание [скрыть]
Нахождение наибольшей нулевой подматрицы
Дана матрица  размером
размером 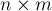 . Требуется найти в ней такую подматрицу, состоящую только из нулей, и среди всех таких — имеющую наибольшую площадь (подматрица — это прямоугольная область матрицы).
. Требуется найти в ней такую подматрицу, состоящую только из нулей, и среди всех таких — имеющую наибольшую площадь (подматрица — это прямоугольная область матрицы).
Тривиальный алгоритм, — перебирающий искомую подматрицу, — даже при самой хорошей реализации будет работать 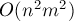 . Ниже описывается алгоритм, работающий за
. Ниже описывается алгоритм, работающий за 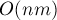 , т.е. за линейное относительно размеров матрицы время.
, т.е. за линейное относительно размеров матрицы время.
Алгоритм
Для устранения неоднозначностей сразу заметим, что  равно числу строк матрицы
равно числу строк матрицы  , соответственно,
, соответственно, 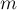 — это число столбцов. Элементы матрицы будем нумеровать в
— это число столбцов. Элементы матрицы будем нумеровать в 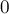 -индексации, т.е. в обозначении
-индексации, т.е. в обозначении ![a[i][j]](../tex2png/cache/60cf76e819ed3733bf887dc748d4b3ef.png) индексы
индексы  и
и  пробегают диапазоны
пробегают диапазоны 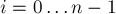 ,
, 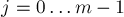 .
.
Шаг 1: Вспомогательная динамика
Сначала посчитаем следующую вспомогательную динамику: ![d[i][j]](../tex2png/cache/a18f11689b09b23faa10c78d6b244cf8.png) — ближайшая сверху единица для элемента
— ближайшая сверху единица для элемента ![a[i][j]](../tex2png/cache/60cf76e819ed3733bf887dc748d4b3ef.png) . Формально говоря,
. Формально говоря, ![d[i][j]](../tex2png/cache/a18f11689b09b23faa10c78d6b244cf8.png) равно наибольшему номеру строки (среди строк диапазоне от
равно наибольшему номеру строки (среди строк диапазоне от 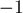 до
до  ), в которой в
), в которой в  -ом столбце стоит единица. В частности, если такой строки нет, то
-ом столбце стоит единица. В частности, если такой строки нет, то ![d[i][j]](../tex2png/cache/a18f11689b09b23faa10c78d6b244cf8.png) полагается равным
полагается равным 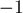 (это можно понимать как то, что вся матрица как будто ограничена снаружи единицами).
(это можно понимать как то, что вся матрица как будто ограничена снаружи единицами).
Эту динамику легко считать двигаясь по матрице сверху вниз: пусть мы стоит в  -ой строке, и известно значение динамики для предыдущей строки. Тогда достаточно скопировать эти значения в динамику для текущей строки, изменив только те элементы, в которых в матрице стоят единицы. Понятно, что тогда даже не требуется хранить всю прямоугольную матрицу динамики, а достаточно только одного массива размера
-ой строке, и известно значение динамики для предыдущей строки. Тогда достаточно скопировать эти значения в динамику для текущей строки, изменив только те элементы, в которых в матрице стоят единицы. Понятно, что тогда даже не требуется хранить всю прямоугольную матрицу динамики, а достаточно только одного массива размера 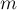 :
:
vector<int> d (m, -1); for (int i=0; i<n; ++i) { for (int j=0; j<m; ++j) if (a[i][j] == 1) d[j] = i; // вычислили d для i-ой строки, можем здесь использовать эти значения }
Шаг 2: Решение задачи
Уже сейчас мы можем решить задачу за 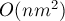 — просто перебирать в текущей строке номер левого и правого столбцов искомой подматрицы, и с помощью динамики
— просто перебирать в текущей строке номер левого и правого столбцов искомой подматрицы, и с помощью динамики ![d[][]](../tex2png/cache/2108d8213526c488460c3eb1fe11c115.png) вычислять за
вычислять за 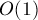 верхнюю границу нулевой подматрицы. Однако можно пойти дальше и значительно улучшить асимптотику решения.
верхнюю границу нулевой подматрицы. Однако можно пойти дальше и значительно улучшить асимптотику решения.
Ясно, что искомая нулевая подматрица ограничена со всех четырёх сторон какими-то единичками (либо границами поля), — которые и мешают ей увеличиться в размерах и улучшить ответ. Поэтому, утверждается, мы не пропустим ответ, если будем действовать следующим образом: сначала переберём номер  нижней строки нулевой подматрицы, затем переберём, в каком столбце
нижней строки нулевой подматрицы, затем переберём, в каком столбце  мы будем упирать вверх нулевую подматрицу. Пользуясь значением
мы будем упирать вверх нулевую подматрицу. Пользуясь значением ![d[i][j]](../tex2png/cache/a18f11689b09b23faa10c78d6b244cf8.png) , мы сразу получаем номер верхней строки нулевой подматрицы. Осталось теперь определить оптимальные левую и правую границы нулевой подматрицы, — т.е. максимально раздвинуть эту подматрицу влево и вправо от
, мы сразу получаем номер верхней строки нулевой подматрицы. Осталось теперь определить оптимальные левую и правую границы нулевой подматрицы, — т.е. максимально раздвинуть эту подматрицу влево и вправо от  -го столбца.
-го столбца.
Что значит раздвинуть максимально влево? Это значит найти такой индекс 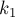 , для которого будет
, для которого будет ![d[i][k_1] > d[i][j]](../tex2png/cache/c37fec2dfb8f0db4773c7f0ab4e48e2a.png) , и при этом
, и при этом 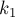 — ближайший такой слева для индекса
— ближайший такой слева для индекса  . Понятно, что тогда
. Понятно, что тогда 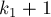 даёт номер левого столбца искомой нулевой подматрицы. Если такого индекса вообще нет, то положить
даёт номер левого столбца искомой нулевой подматрицы. Если такого индекса вообще нет, то положить 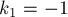 (это означает, что мы смогли расширить текущую нулевую подматрицу влево до упора — до границы всей матрицы
(это означает, что мы смогли расширить текущую нулевую подматрицу влево до упора — до границы всей матрицы  ).
).
Симметрично можно определить индекс 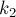 для правой границы: это ближайший справа от
для правой границы: это ближайший справа от  индекс такой, что
индекс такой, что ![d[i][k_2] > d[i][j]](../tex2png/cache/dd79bfe1cafc6a3b87c30ffe3ee219ac.png) (либо
(либо 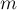 , если такого индекса нет).
, если такого индекса нет).
Итак, индексы 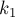 и
и 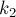 , если мы научимся эффективно их искать, дадут нам всю необходимую информацию о текущей нулевой подматрице. В частности, её площадь будет равна
, если мы научимся эффективно их искать, дадут нам всю необходимую информацию о текущей нулевой подматрице. В частности, её площадь будет равна ![(i - d[i][j]) \cdot (k_2 - k_1 - 1)](../tex2png/cache/ce35c248ff8902f74814021e5e031fc7.png) .
.
Как же искать эти индексы 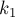 и
и 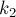 эффективно при фиксированных
эффективно при фиксированных  и
и  ? Нас удовлетворит только асимптотика
? Нас удовлетворит только асимптотика 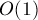 , хотя бы в среднем.
, хотя бы в среднем.
Добиться такой асимптотики можно с помощью стека (stack) следующим образом. Научимся сначала искать индекс 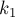 , и сохранять его значение для каждого индекса
, и сохранять его значение для каждого индекса  внутри текущей строки
внутри текущей строки  в динамике
в динамике ![d_1[i][j]](../tex2png/cache/32430566c4aab71fcece1881523c359a.png) . Для этого будем просматривать все столбцы
. Для этого будем просматривать все столбцы  слева направо, и заведём такой стек, в котором всегда будут лежать только те столбцы, в которых значение динамики
слева направо, и заведём такой стек, в котором всегда будут лежать только те столбцы, в которых значение динамики ![d[][]](../tex2png/cache/2108d8213526c488460c3eb1fe11c115.png) строго больше
строго больше ![d[i][j]](../tex2png/cache/a18f11689b09b23faa10c78d6b244cf8.png) . Понятно, что при переходе от столбца
. Понятно, что при переходе от столбца  к следующему столбцу
к следующему столбцу 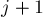 требуется обновить содержимое этого стека. Утверждается, что требуется сначала положить в стек столбец
требуется обновить содержимое этого стека. Утверждается, что требуется сначала положить в стек столбец  (поскольку для него стек "хороший"), а затем, пока на вершине стека лежит неподходящий элемент (т.е. у которого значение
(поскольку для него стек "хороший"), а затем, пока на вершине стека лежит неподходящий элемент (т.е. у которого значение ![d \le d[i][j+1]](../tex2png/cache/7626da875d0916986ff685e9a127990f.png) ), — доставать этот элемент. Легко понять, что удалять из стека достаточно только из его вершины, и ни из каких других его мест (потому что стек будет содержать возрастающую по
), — доставать этот элемент. Легко понять, что удалять из стека достаточно только из его вершины, и ни из каких других его мест (потому что стек будет содержать возрастающую по 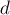 последовательность столбцов).
последовательность столбцов).
Значение ![d_1[i][j]](../tex2png/cache/32430566c4aab71fcece1881523c359a.png) для каждого
для каждого  будет равно значению, лежащему в этот момент на вершине стека.
будет равно значению, лежащему в этот момент на вершине стека.
Ясно, что поскольку добавлений в стек на каждой строчке  происходит ровно
происходит ровно 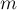 штук, то и удалений также не могло быть больше, поэтому в сумме асимптотика будет линейной.
штук, то и удалений также не могло быть больше, поэтому в сумме асимптотика будет линейной.
Динамика ![d_2[i][j]](../tex2png/cache/54bcf310c049860b37bf7cf8251d8154.png) для нахождения индексов
для нахождения индексов 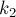 считается аналогично, только надо просматривать столбцы справа налево.
считается аналогично, только надо просматривать столбцы справа налево.
Также следует отметить, что этот алгоритм потребляет 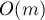 памяти (не считая входные данные — матрицу
памяти (не считая входные данные — матрицу ![a[][]](../tex2png/cache/f9fa957c4ed546b728381d1556189238.png) ).
).
Реализация
Эта реализация вышеописанного алгоритма считывает размеры матрицы, затем саму матрицу (как последовательность чисел, разделённых пробелами или переводами строк), и затем выводит ответ — размер наибольшей нулевой подматрицы.
Легко улучшить эту реализацию, чтобы она также выводила саму нулевую подматрицу: для этого надо при каждом изменении 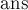 запоминать также номера строк и столбцов подматрицы (ими будут соответственно
запоминать также номера строк и столбцов подматрицы (ими будут соответственно ![d[j]+1](../tex2png/cache/16feed5b0bc695d7a84bb7ac1d73668d.png) ,
,  ,
, ![d1[j]+1](../tex2png/cache/ca1e1eb142ee98304e7d6bfe8bcf1f15.png) ,
, ![d2[j]-1](../tex2png/cache/5e3709fa4e0d6b252ea104c8114c81f1.png) ).
).
int n, m; cin >> n >> m; vector < vector<int> > a (n, vector<int> (m)); for (int i=0; i<n; ++i) for (int j=0; j<m; ++j) cin >> a[i][j]; int ans = 0; vector<int> d (m, -1), d1 (m), d2 (m); stack<int> st; for (int i=0; i<n; ++i) { for (int j=0; j<m; ++j) if (a[i][j] == 1) d[j] = i; while (!st.empty()) st.pop(); for (int j=0; j<m; ++j) { while (!st.empty() && d[st.top()] <= d[j]) st.pop(); d1[j] = st.empty() ? -1 : st.top(); st.push (j); } while (!st.empty()) st.pop(); for (int j=m-1; j>=0; --j) { while (!st.empty() && d[st.top()] <= d[j]) st.pop(); d2[j] = st.empty() ? m : st.top(); st.push (j); } for (int j=0; j<m; ++j) ans = max (ans, (i - d[j]) * (d2[j] - d1[j] - 1)); } cout << ans;