MAXimal
добавлено: 17 Jul 2009 23:00
редактировано: 17 Jul 2009 23:00
Содержание [скрыть]
Рандомизированная куча
Рандомизированная куча (randomized heap) — это куча, которая за счёт применения генератора случайных чисел позволяет выполнять все необходимые операции за логарифмическое ожидаемое время.
Кучей называется бинарное дерево, для любой вершины которого справедливо, что значение в этой вершине меньше либо равно значений во всех её потомках (это куча для минимума; разумеется, симметрично можно определить кучу для максимума). Таким образом, в корне кучи всегда находится минимум.
Стандартный набор операций, определяемый для куч, следующий:
- Добавление элемента
- Нахождение минимума
- Извлечение минимума (удаление его из дерева и возврат его значения)
- Слияние двух куч (возвращается куча, содержащая элементы обеих куч; дубликаты не удаляются)
- Удаление произвольного элемента (при известной позиции в дереве)
Рандомизированная куча позволяет выполнять все эти операции за ожидаемое время 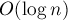 при очень простой реализации.
при очень простой реализации.
Структура данных
Сразу опишем структуру данных, описывающую бинарную кучу:
struct tree { T value; tree * l, * r; };В вершине дерева хранится значение
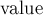 некоторого типа
некоторого типа 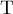 , для которого определён оператор сравнения (
, для которого определён оператор сравнения (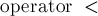 ). Кроме того, хранятся указатели на левого и правого сыновей (которые равны 0, если соответствующий сын отсутствует).
). Кроме того, хранятся указатели на левого и правого сыновей (которые равны 0, если соответствующий сын отсутствует).Выполнение операций
Нетрудно понять, что все операции над кучей сводятся к одной операции: слиянию двух куч в одну. Действительно, добавление элемента в кучу равносильно слиянию этой кучи с кучей, состоящей из единственного добавляемого элемента. Нахождение минимума вообще не требует никаких действий — минимумом просто является корень кучи. Извлечение минимума эквивалентно тому, что куча заменяется результатом слияния левого и правого поддерева корня. Наконец, удаление произвольного элемента аналогично удалению минимума: всё поддерево с корнем в этой вершине заменяется результатом слияния двух поддеревьев-сыновей этой вершины.
Итак, нам фактически надо реализовать только операцию слияния двух куч, все остальные операции тривиально сводятся к этой операции.
Пусть даны две кучи 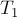 и
и 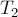 , требуется вернуть их объединение. Понятно, что в корне каждой из этих куч находятся их минимумы, поэтому в корне результирующей кучи будет находиться минимум из этих двух значений. Итак, мы сравниваем, в корне какой из куч находится меньшее значение, его помещаем в корень результата, а теперь мы должны объединить сыновей выбранной вершины с оставшейся кучей. Если мы по какому-то признаку выберем одного из двух сыновей, то тогда нам надо будет просто объединить поддерево в корне с этим сыном с кучей. Таким образом, мы снова пришли к операции слияния. Рано или поздно этот процесс остановится (на это понадобится, понятно, не более чем сумма высот куч).
, требуется вернуть их объединение. Понятно, что в корне каждой из этих куч находятся их минимумы, поэтому в корне результирующей кучи будет находиться минимум из этих двух значений. Итак, мы сравниваем, в корне какой из куч находится меньшее значение, его помещаем в корень результата, а теперь мы должны объединить сыновей выбранной вершины с оставшейся кучей. Если мы по какому-то признаку выберем одного из двух сыновей, то тогда нам надо будет просто объединить поддерево в корне с этим сыном с кучей. Таким образом, мы снова пришли к операции слияния. Рано или поздно этот процесс остановится (на это понадобится, понятно, не более чем сумма высот куч).
Таким образом, чтобы достичь логарифмической асимптотики в среднем, нам надо указать способ выбора одного из двух сыновей с тем, чтобы в среднем длина проходимого пути получалась бы порядка логарифма от количества элементов в куче. Нетрудно догадаться, что производить этот выбор мы будем случайно, таким образом, реализация операции слияния получается такой:
tree * merge (tree * t1, tree * t2) { if (!t1 || !t2) return t1 ? t1 : t2; if (t2->value < t1->value) swap (t1, t2); if (rand() & 1) swap (t1->l, t1->r); t1->l = merge (t1->l, t2); return t1; }
Здесь сначала проверяется, если хотя бы одна из куч пуста, то никаких действий по слиянию производить не надо. Иначе, мы делаем, чтобы куча 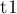 была кучей с меньшим значением в корне (для чего обмениваем
была кучей с меньшим значением в корне (для чего обмениваем 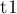 и
и 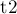 , если надо). Наконец, мы считаем, что вторую кучу
, если надо). Наконец, мы считаем, что вторую кучу 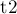 будем сливать с левым сыном корня кучи
будем сливать с левым сыном корня кучи 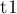 , поэтому мы случайным образом обмениваем левого и правого сыновей, а затем выполняем слияние левого сына и второй кучи.
, поэтому мы случайным образом обмениваем левого и правого сыновей, а затем выполняем слияние левого сына и второй кучи.
Асимптотика
Введём случайную величину 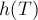 , обозначающую длину случайного пути от корня до листа (длина в числе рёбер). Понятно, что алгоритм
, обозначающую длину случайного пути от корня до листа (длина в числе рёбер). Понятно, что алгоритм 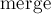 выполняется за
выполняется за 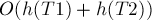 операций. Поэтому для исследования асимптотики алгоритма надо исследовать случайную величину
операций. Поэтому для исследования асимптотики алгоритма надо исследовать случайную величину 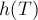 .
.
Математическое ожидание
Утверждается, что математическое ожидание 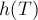 оценивается сверху логарифмом от числа
оценивается сверху логарифмом от числа  вершин в этой куче:
вершин в этой куче:
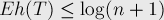
Доказывается это легко по индукции. Пусть 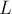 и
и 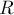 — соответственно левое и правое поддеревья корня кучи
— соответственно левое и правое поддеревья корня кучи 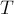 , а
, а 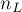 и
и 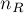 — количества вершин в них (понятно, что
— количества вершин в них (понятно, что 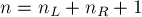 ).
).
Тогда справедливо:
![Eh(T) = 1 + \frac{1}{2}(Eh(L) + Eh(R)) \le 1 + \f[...]](../tex2png/cache/616dd1b71828904a200f8322d05836ef.png)
![= 1 + \log \sqrt{ (n_L+1)(n_R+1) } = \log 2 \sqrt[...]](../tex2png/cache/d5820bf5a9ac49f8e0012d26d8b09e14.png)
![\le \log \frac{ 2 ((n_L+1) + (n_R+1)) }{ 2 } = \l[...]](../tex2png/cache/88478fe624acafa82531eb8555ad4feb.png)
Превышение ожидаемой оценки
Докажем, что вероятность превышения полученной выше оценки мала:
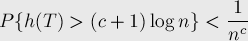
 .
.Обозначим через  множество путей от корня кучи до листьев, длина которых превосходит
множество путей от корня кучи до листьев, длина которых превосходит 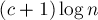 . Заметим, что для любого пути
. Заметим, что для любого пути 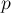 длины
длины 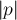 вероятность того, в качестве случайного пути будет выбран именно он, равна
вероятность того, в качестве случайного пути будет выбран именно он, равна 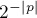 . Тогда получаем:
. Тогда получаем:
![P\{ h(T) > (c+1) \log n \} = \sum_{p \in P} 2^{-|[...]](../tex2png/cache/1988902add42dd0242a03193baa2b52d.png)
Асимптотика алгоритма
Таким образом, алгоритм 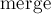 , а, значит, и все остальные выраженные через него операции, выполняется за
, а, значит, и все остальные выраженные через него операции, выполняется за 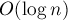 в среднем.
в среднем.
Более того, для любой положительной константы 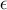 найдётся такая положительная константа
найдётся такая положительная константа  , что вероятность того, что операция потребует больше чем
, что вероятность того, что операция потребует больше чем 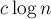 операций, меньше
операций, меньше 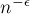 (это в некотором смысле описывает худшее поведение алгоритма).
(это в некотором смысле описывает худшее поведение алгоритма).