Метод Ньютона (касательных) для поиска корней

Это итерационный метод, изобретённый Исааком Ньютоном (Isaak Newton) около 1664 г. Впрочем, иногда этот метод называют методом Ньютона-Рафсона (Raphson), поскольку Рафсон изобрёл тот же самый алгоритм на несколько лет позже Ньютона, однако его статья была опубликована намного раньше.

Задача заключается в следующем. Дано уравнение:

$f(x) = 0.$

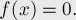
Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что корень существует). Предполагается, что 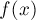$f(x)$ непрерывна и дифференцируема на отрезке $[a;b]$ .

Алгоритм

Входным параметром алгоритма, кроме функции 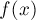$f(x)$ , является также начальное приближение — некоторое 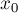$x_0$ , от которого алгоритм начинает идти.

Пусть уже вычислено 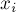$x_i$ , вычислим 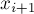$x_{i+1}$ следующим образом. Проведём касательную к графику функции 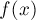$f(x)$ в точке 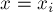$x = x_i$ , и найдём точку пересечения этой касательной с осью абсцисс. 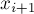$x_{i+1}$ положим равным найденной точке, и повторим весь процесс с начала.

Нетрудно получить следующую формулу:

$x_{i+1} = x_i - \frac{ f(x_i) }{ f^\prime(x_i) }.[...]$

Интуитивно ясно, что если функция 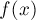$f(x)$ достаточно "хорошая" (гладкая), а 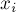$x_i$ находится достаточно близко от корня, то 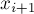$x_{i+1}$ будет находиться ещё ближе к искомому корню.

Скорость сходимости является квадратичной, что, условно говоря, означает, что число точных разрядов в приближенном значении 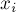$x_i$ удваивается с каждой итерацией.

Применение для вычисления квадратного корня

Рассмотрим метод Ньютона на примере вычисления квадратного корня.

Если подставить 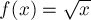$f(x) = \sqrt{x}$ , то после упрощения выражения получаем:

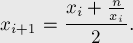
$x_{i+1} = \frac{ x_i + \frac{n}{x_i} }{ 2 }.$

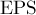Первый типичный вариант задачи — когда дано дробное число $n$ , и нужно подсчитать его корень с некоторой точностью $\rm EPS$ :

double n;
cin >> n;
const double EPS = 1E-15;
double x = 1;
for (;;) {
	double nx = (x + n / x) / 2;
	if (abs (x - nx) < EPS)  break;
	x = nx;
}
printf ("%.15lf", x);

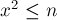Другой распространённый вариант задачи — когда требуется посчитать целочисленный корень (для данного $n$ найти наибольшее $x$ такое, что $x^2 \le n$ ). Здесь приходится немного изменять условие останова алгоритма, поскольку может случиться, что $x$ начнёт "скакать" возле ответа. Поэтому мы добавляем условие, что если значение $x$ на предыдущем шаге уменьшилось, а на текущем шаге пытается увеличиться, то алгоритм надо остановить.

int n;
cin >> n;
int x = 1;
bool decreased = false;
for (;;) {
	int nx = (x + n / x) >> 1;
	if (x == nx || nx > x && decreased)  break;
	decreased = nx < x;
	x = nx;
}
cout << x;

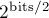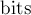Наконец, приведём ещё третий вариант — для случая длинной арифметики. Поскольку число $n$ может быть достаточно большим, то имеет смысл обратить внимание на начальное приближение. Очевидно, что чем оно ближе к корню, тем быстрее будет достигнут результат. Достаточно простым и эффективным будет брать в качестве начального приближения число $2^{{\rm bits}/2}$ , где $\rm bits$ — количество битов в числе $n$ . Вот код на языке Java, демонстрирующий этот вариант:

BigInteger n; // входные данные
 
BigInteger a = BigInteger.ONE.shiftLeft (n.bitLength() / 2);
boolean p_dec = false;
for (;;) {
	BigInteger b = n.divide(a).add(a).shiftRight(1);
	if (a.compareTo(b) == 0 || a.compareTo(b) < 0 && p_dec)  break;
	p_dec = a.compareTo(b) > 0;
	a = b;
}

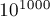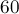Например, этот вариант кода выполняется для числа $10^{1000}$ за $60$ миллисекунд, а если убрать улучшенный выбор начального приближения (просто начинать с 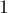$1$ ), то будет выполняться примерно 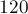$120$ миллисекунд.