Топологическая сортировка

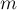Дан ориентированный граф с $n$ вершинами и $m$ рёбрами. Требуется перенумеровать его вершины таким образом, чтобы каждое рёбро вело из вершины с меньшим номером в вершину с большим.

Иными словами, требуется найти перестановку вершин (топологический порядок), соответствующую порядку, задаваемому всеми рёбрами графа.

Топологическая сортировка может быть не единственной (например, если граф — пустой; или если есть три такие вершины $a$ , $b$ , $c$ , что из $a$ есть пути в $b$ и в $c$ , но ни из $b$ в $c$ , ни из $c$ в $b$ добраться нельзя).

Топологической сортировки может не существовать вовсе — если граф содержит циклы (поскольку при этом возникает противоречие: есть путь и из одной вершины в другую, и наоборот).

Распространённая задача на топологическую сортировку — следующая. Есть $n$ переменных, значения которых нам неизвестны. Известно лишь про некоторые пары переменных, что одна переменная меньше другой. Требуется проверить, не противоречивы ли эти неравенства, и если нет, выдать переменные в порядке их возрастания (если решений несколько — выдать любое). Легко заметить, что это в точности и есть задача о поиске топологической сортировки в графе из $n$ вершин.

Алгоритм

Для решения воспользуемся обходом в глубину.

Предположим, что граф ацикличен, т.е. решение существует. Что делает обход в глубину? При запуске из какой-то вершины $v$ он пытается запуститься вдоль всех рёбер, исходящих из $v$ . Вдоль тех рёбер, концы которых уже были посещены ранее, он не проходит, а вдоль всех остальных — проходит и вызывает себя от их концов.

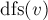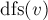Таким образом, к моменту выхода из вызова ${\rm dfs}(v)$ все вершины, достижимые из $v$ как непосредственно (по одному ребру), так и косвенно (по пути) — все такие вершины уже посещены обходом. Следовательно, если мы будем в момент выхода из ${\rm dfs}(v)$ добавлять нашу вершину в начало некоего списка, то в конце концов в этом списке получится топологическая сортировка.

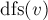Эти объяснения можно представить и в несколько ином свете, с помощью понятия "времени выхода" обхода в глубину. Время выхода для каждой вершины $v$ — это момент времени, в который закончил работать вызов ${\rm dfs}(v)$ обхода в глубину от неё (времена выхода можно занумеровать от 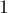$1$ до $n$ ). Легко понять, что при обходе в глубину время выхода из какой-либо вершины $v$ всегда больше, чем время выхода из всех вершин, достижимых из неё (т.к. 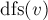они были посещены либо до вызова ${\rm dfs}(v)$ , либо во время него). Таким образом, искомая топологическая сортировка — это сортировка в порядке убывания времён выхода.

Реализация

Приведём реализацию, предполагающую, что граф ацикличен, т.е. искомая топологическая сортировка существует. При необходимости проверку графа на ацикличность легко вставить в обход в глубину, как описано в статье по обходу в глубину.

int n; // число вершин
vector<int> g[MAXN]; // граф
bool used[MAXN];
vector<int> ans;
 
void dfs (int v) {
	used[v] = true;
	for (size_t i=0; i<g[v].size(); ++i) {
		int to = g[v][i];
		if (!used[to])
			dfs (to);
	}
	ans.push_back (v);
}
 
void topological_sort() {
	for (int i=0; i<n; ++i)
		used[i] = false;
	ans.clear();
	for (int i=0; i<n; ++i)
		if (!used[i])
			dfs (i);
	reverse (ans.begin(), ans.end());
}

Здесь константе 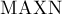$\rm MAXN$ следует задать значение, равное максимально возможному числу вершин в графе.

Основная функция решения — это topological_sort, она инициализирует пометки обхода в глубину, запускает его, и ответ в итоге получается в векторе 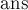$\rm ans$ .

Задачи в online judges

Список задач, в которых требуется искать топологическую сортировку: